MUSIC AND MATHEMATICS
Today, let’s talk about music and mathematics. The University of Houston’s Math Department presents this program about the machines that make our civilization run, and the people whose ingenuity created them. The history of musical instruments goes back tens of thousands of years. Fragments of bone flutes have been found at Neanderthal sites. Early instruments show that humans have long produced pitched sound — sound containing predominantly a single frequency. Finger holes on ancient flutes indicate that prehistoric musicians had some concept of a musical scale.
Music is also the most mathematical art. Already the Pythagoreans of ancient Greece studied the mathematics of musical instruments. According to legend, Pythagoras was listening to blacksmiths at work. He noticed that some of their hammers produced a pleasing combination of sounds when struck together. When he examined these hammers he found that one weighed 12 pounds and another 6 pounds. The first hammer weighed exactly twice as much as the second.

Pythagoras had discovered a fundamental principle of harmony. Most Western instruments produce sound by causing air to vibrate a certain number of times per second. When two instruments cause air to vibrate at frequencies whose ratios form simple fractions — 2:1 or 3:2, say — we perceive a pleasing combination of sounds. The consonance between the blacksmith’s hammers caught Pythagoras’ attention. For instance, the 6 pound hammer produced vibrations exactly twice as fast as those of the 12 pound hammer. This two-to-one relationship between notes is called an octave, and appears in nearly all music produced by humankind.
But, the problem of translating Pythagoras’ observations to the design a musical instruments has bedeviled some of the brightest minds of millennia past. How do we tune a piano, or any ensemble instrument, so it sounds good when it’s played with other instruments?

Hundreds of different tunings have been proposed to work around this problem. Bach wrote his Well-Tempered Clavier to demonstrate the advantage of a slightly imperfect tuning he favored. With past tunings some music sounded very pleasing, while other compositions could sound woefully out of tune. In nearly all music today we use equal temperament — a compromise that effectively makes all our music sound equally pleasing, or equally out of tune – depending on your perspective.
The next time you consider the cold rationality of mathematics, also remember that math is behind the sound of violins, pianos, and song. The beauty of mathematics shines through in the music it helps us create.

Numerous websites explain the basics of harmony. Here is a very simple explanation that includes an example with sound http://www.aboutscotland.co.uk/harmony/prop.html.
You can find more about the mathematics of musical instruments in the following article that appear in the American Mathematical Monthly: http://www.math.uh.edu/~josic/myweb/research/papers/mathandmusic.pdf.
Although idiosyncratic, I like Bill Sethares’ approach to tuning. He shows how modern technology allows us to easily create scales with any number of notes. There are some pretty interesting examples on his webpage http://eceserv0.ece.wisc.edu/~sethares/.
The story of the Neanderthal flute has been discussed previously in this series http://www.uh.edu/engines/epi1232.htm. However, the finding remains very controversial http://en.wikipedia.org/wiki/Divje_Babe_flute.
All images are in the Creative Commons.
The Engines of Our Ingenuity is Copyright © 1988-2010 by John H. Lienhard.
Engines of Our Ingenuity http://uh.edu/engines/epi2579.htm
ππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππππ
The Pythagorean Theorem
SOURCE: http://www.mathwarehouse.com/geometry/triangles/right-triangle.html
The Pythagorean Theorem computes the hypotenuse of a right triangle using the following relationship between the legs and the hypotenuse of a triangle:
The hypotenuse [c] equals the square root of the sum of the squares of each leg of the triangle [a and b].
Right Triangles and The Good Old Pythagorean Theorem
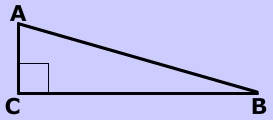 | A right triangle has one 90° angle and a variety of often-studied properties such as: ��� |
A Right Triangle's Hypotenuse
The hypotenuse is the largest side in a right triangle and is always opposite the right angle. (Only right triangles have a hypotenuse). The other two sides of the triangle, AC and CB are referred to as the 'legs'. 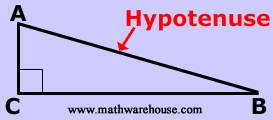 In the triangle on the left, the hypotenuse is the side AB which is opposite the right angle, angle |
The pythagorean theorem : the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse.
- Usually, this theorem is expressed as a2+b2=c2
 | In the right triangle on the left, A2+ B2= C2 |
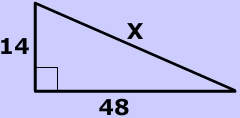 | What is the value of x in the picture on the left?
142 + 482 = x2 2,500 =X2 |
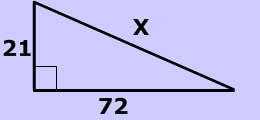 | What is the value of x in the picture on the left?
x2 = 5,625 |
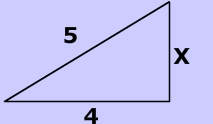 | What is x in the triangle on the left?
X2 +16=25 X2 = 25 - 16 X= 3 |
No comments:
Post a Comment